算法训练——找出游戏的获胜者(约瑟夫环)

题目描述

共有 n 名小伙伴一起做游戏。小伙伴们围成一圈，按 顺时针顺序 从 1 到 n 编号。确切地说，从第 i 名小伙伴顺时针移动一位会到达第 (i+1) 名小伙伴的位置，其中 1 <= i < n ，从第 n 名小伙伴顺时针移动一位会回到第 1 名小伙伴的位置。

游戏遵循如下规则：

从第 1 名小伙伴所在位置开始。
沿着顺时针方向数 k 名小伙伴，计数时需要包含起始时的那位小伙伴。逐个绕圈进行计数，一些小伙伴可能会被数过不止一次。
你数到的最后一名小伙伴需要离开圈子，并视作输掉游戏。
如果圈子中仍然有不止一名小伙伴，从刚刚输掉的小伙伴的 顺时针下一位 小伙伴开始，回到步骤 2 继续执行。
否则，圈子中最后一名小伙伴赢得游戏。

给你参与游戏的小伙伴总数 n ，和一个整数 k ，返回游戏的获胜者。

示例 1：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


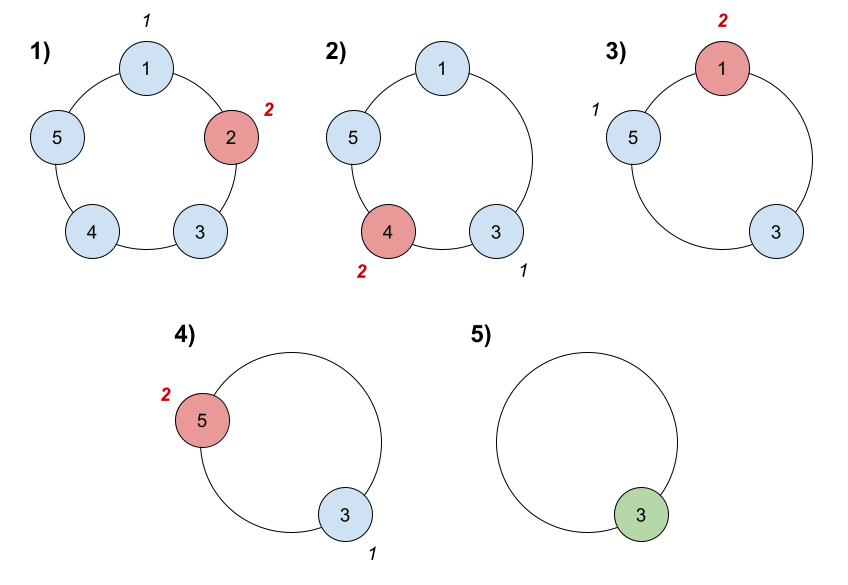
输入：n = 5, k = 2
输出：3
解释：游戏运行步骤如下：
1) 从小伙伴 1 开始。
2) 顺时针数 2 名小伙伴，也就是小伙伴 1 和 2 。
3) 小伙伴 2 离开圈子。下一次从小伙伴 3 开始。
4) 顺时针数 2 名小伙伴，也就是小伙伴 3 和 4 。
5) 小伙伴 4 离开圈子。下一次从小伙伴 5 开始。
6) 顺时针数 2 名小伙伴，也就是小伙伴 5 和 1 。
7) 小伙伴 1 离开圈子。下一次从小伙伴 3 开始。
8) 顺时针数 2 名小伙伴，也就是小伙伴 3 和 5 。
9) 小伙伴 5 离开圈子。只剩下小伙伴 3 。所以小伙伴 3 是游戏的获胜者。

示例 2：

1
2
3


输入：n = 6, k = 5
输出：1
解释：小伙伴离开圈子的顺序：5、4、6、2、3 。小伙伴 1 是游戏的获胜者。

提示：

1 <= k <= n <= 500

进阶： 你能否使用线性时间复杂度和常数空间复杂度解决此问题？

解题过程

思路

这是一个很典型的约瑟夫环的问题。用队列可以很简单的解决。

先将n个人入队列，然后依次出队列的同时再入队，当到第k个人的时候出队列不再入队。

剩下的最后一个人即为获胜者。

代码实现

Java

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


class Solution {
    public static int findTheWinner(int n, int k) {
        Queue<Integer> q = new ArrayDeque<>();/*需导包java.util.ArrayDeque和java.util.Queue*/
        for (int i = 1; i <= n; i++) {/*初始化队列*/
            q.offer(i);
        }
        while (q.size() > 1) {
            for (int i = 1; i < k; i++) {
                q.offer(q.poll());/*出队再入队*/
            }
            q.poll();/*第k位即为淘汰者*/
        }
        return q.peek();/*最后剩下获胜者*/
    }
}

C

c语言并不自带队列的计算方法，待一段时间后等我学会再补上。

其他方法

由于存在一定的数学规律，也可以通过公式法或者迭代函数的方法求解。

这里引用官方的题解。

方法二：数学 + 递归

以下用 f(n,k) 表示 n 名小伙伴做游戏，每一轮离开圈子的小伙伴的计数为 k 时的获胜者编号。

当 n=1 时，圈子中只有一名小伙伴，该小伙伴即为获胜者，因此 f(1,k)=1。

当 n>1 时，将有一名小伙伴离开圈子，圈子中剩下 n−1 名小伙伴。圈子中的第 k ′名小伙伴离开圈子，k ′满足 1≤k′≤n 且 k−k′是 n 的倍数。

由于 1≤k′≤n，因此 0≤k′−1≤n−1。又由于 k−k’是 n 的倍数等价于 (k−1)−(k′−1) 是 n 的倍数，因此 k′−1=(k−1)modn，k′=(k−1)modn+1。

当圈子中剩下 n−1 名小伙伴时，可以递归地计算 f(n−1,k)，得到剩下的 n−1 名小伙伴中的获胜者。令 x=f(n−1,k)。

由于在第 k′名小伙伴离开圈子之后，圈子中剩下的 n−1 名小伙伴从第 k′+1 名小伙伴开始计数，获胜者编号是从第 k′+1 名小伙伴开始的第 x 名小伙伴，因此当圈子中有 n 名小伙伴时，获胜者编号是 f(n,k)=(k’modn+x−1)modn+1=(k+x−1)modn+1。

将 x=f(n−1,k) 代入上述关系，可得：f(n,k)=(k+f(n−1,k)−1)modn+1。

java

1
2
3
4
5
6
7
8


class Solution {
    public int findTheWinner(int n, int k) {
        if (n == 1) {
            return 1;
        }
        return (k + findTheWinner(n - 1, k) - 1) % n + 1;
    }
}

1
2
3
4
5
6


int findTheWinner(int n, int k){
    if (n == 1) {
        return 1;
    }
    return (k + findTheWinner(n - 1, k) - 1) % n + 1;
}

方法三：数学 + 迭代

方法二的递归实现可以改成迭代实现，省略递归调用栈空间。

java

1
2
3
4
5
6
7
8
9


class Solution {
    public int findTheWinner(int n, int k) {
        int winner = 1;
        for (int i = 2; i <= n; i++) {
            winner = (k + winner - 1) % i + 1;
        }
        return winner;
    }
}

1
2
3
4
5
6
7


int findTheWinner(int n, int k){
    int winner = 1;
    for (int i = 2; i <= n; i++) {
        winner = (k + winner - 1) % i + 1;
    }
    return winner;
}